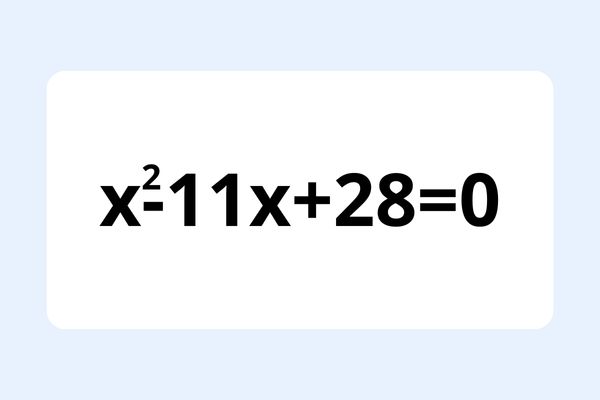Introducing a tour of quadratic equations of fundamental components of algebra and mathematics. we will explore the topic of quadratic equations in this article, concentrating on the equation x2-11x+28=0.
In this in-depth conversation, we will address the fundamental Idea behind the education of quadratic equations, investigate various approaches to their solution, and delve deeply into a particular case study to comprehend the real-world uses of these equations.
So, let’s find out some basic facts about quadratic equations.
A Quadratic Equation: What is it?
Before we set out on this journey, let’s understand what a quadratic equation is. the squared variable, Which is a property of second-degree polynomials, defines a quadratic equation. An expression for a quadratic equation in its most basic form is:
ax^2 + bx + c = 0
X denotes the variable in the equation and ‘a’, ‘b’, and ‘c’ stands for the coefficients. The formula x2-11x+28=0 is exactly in this standard form.
Well! It was just the central principle of quadratic equations, but it has its other form too. Let’s move to the next part where we will discuss another form of quadratic equations and delve into its graphical representation.
A Quadratic Equation (x2-11x+28=0) in Its General Form
Understanding the general structure of a quadratic equation is critical since it forms the basis of these equations. Recognizing this structure allows us to easily identify the coefficients ‘a’, ‘b’, and ‘c’. For our particular equation, ‘a’ equals 1, ‘b’ equals -11, and ‘c’ equals 28.
x2-11x+28=0: Solving Quadratic Equation
Quadratic equations are a class of mathematical problems that may be solved using a variety of techniques. Let’s look at three popular techniques:
Factoring
Factoring is a technique for solving quadratic equations that can be readily split down. However, factoring may not be the easiest solution for equations as complicated as x2-11x+28=0.
Quadratic Formula
The quadratic formula emerges as an adaptable and globally applicable method for solving quadratic problems. This formula, which is frequently used, is:
x = (-b ± √(b^2 – 4ac)) / 2a
This formula yields the equation’s roots, which reflect the numerical values of ‘x’ that make the equation equivalent to zero.
Trigonometric Solution
Within this perspective, we may comprehend the evolution of methods for solving quadratic equations using trigonometric substitution. Consider the following alternative quadratic equation form:
ax^2 + bx ± c = 0
where the symbol ± is selected so that a and c can both be positive. By substituting.
x= cθ
and then multiplying it by cos2(θ) / c, we get
Sin2θ + b/ac Sinθ cosθ ± cos2θ = 0.
The effort required to solve quadratic equations using this hybrid trigonometric and logarithmic table look-up technique was two-thirds of that required using logarithmic tables alone. Complex roots would necessitate the use of a different trigonometric expression.
Case Study: x2-11x+28=0
We now shift our attention to the intriguing equation x2-11x+28=0. Our investigation will include a step-by-step study of the quadratic formula.
- Step 1: Find the Coefficients
To begin this voyage, we must first determine the coefficients. In the given equation, ‘a’ equals 1, ‘b’ equals -11, and ‘c’ equals 28.
- Step 2: Use the Quadratic Formula
Now that we have the coefficients, we can use the quadratic formula. The equation looks like this:
x = (-(-11) ± √((-11)^2 – 4 * 1 * 28)) / (2 * 1)
To get a solution, we simplify the equation, resulting in:
x = (11 ± √(121 – 112)) / 2
x = (11 ± √9) / 2
- Step 3: Discovering the roots
We discover two alternative solutions as the problem begins to crystallize:
x = (11 + 3) / 2 = 7
x = (11 – 3) / 2 = 4
As a result, the roots of the equation x2-11x+28=0 are x = 7 and x = 4.
Graphical representation of Quadratic Equations
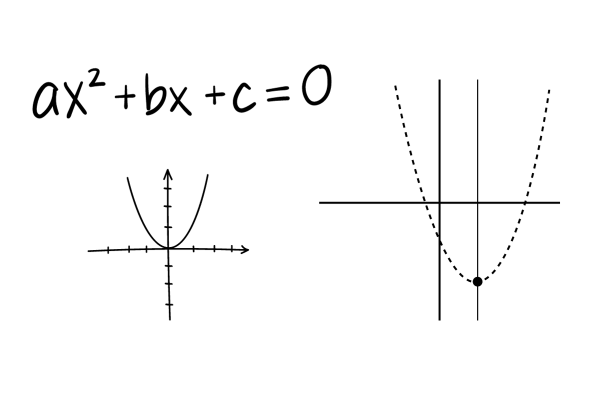
The graphical representation of quadratic equations is frequently in the shape of a parabola. The U-shaped curve reveals important information about the behavior of these equations, with the vertex being a central point that represents either the lowest or highest point of the parabola.
- The points where the quadratic polynomial’s value is zero, or where the parabola crosses the x-axis, are the roots of a quadratic equation.
If ax2+bx+c is a quadratic polynomial then,
- The parabola widens upward if a>0.
- The parabola opens downward if a<0. The polynomial becomes a first-degree polynomial and has a linear graph if a = 0.
And nature of the graph for different values of the discriminant, D=b2−4ac, is
- The parabola intersects the x-axis at precisely two spots if D>0. There are distinct roots.
- When D=0, the parabola only contacts the x-axis once, with the remaining portion of the parabola lying either above or below it. The roots in this instance are equal.
- There is no point of contact with the x-axis and the parabola rests completely above or below it if D<0. Here, there aren’t any true roots.
Applications of Quadratic Equations
 The usefulness of quadratic equations extends beyond theory, with applications in physics, engineering, and economics.
The usefulness of quadratic equations extends beyond theory, with applications in physics, engineering, and economics.
It is possible to compute values for both stationary and moving objects or items using certain quadratic equations.
When an item is in motion, we may determine its maximum height, its reaching point, its distance from specific spots at specific periods, and so forth.
Quadratic equations are also effective tools for modeling and solving difficulties in various real-world contexts such as when determining the areas of enclosed spaces, the speed of objects, a product’s profit and loss, or the curvature of equipment for design purposes.
Conclusion
Exploring the world of quadratic equations has been a wonderful experience. We have unwrapped the underlying principles underlying quadratic equations, and the approach to tackling them using the quadratic formula, and experienced the practical ramifications through a particular case study, namely x2-11x+28=0, in this article.
Additionally, we have examined how quadratic equations may be visually represented using parabolic graphs and have emphasized the practical significance of these representations in a range of applications.